В данной статье мы рассмотрим интересное математическое доказательство, связанное с четырехугольником ABCD и треугольниками АВС и СВАУ. Мы покажем, что эти два треугольника равны друг другу.




































































































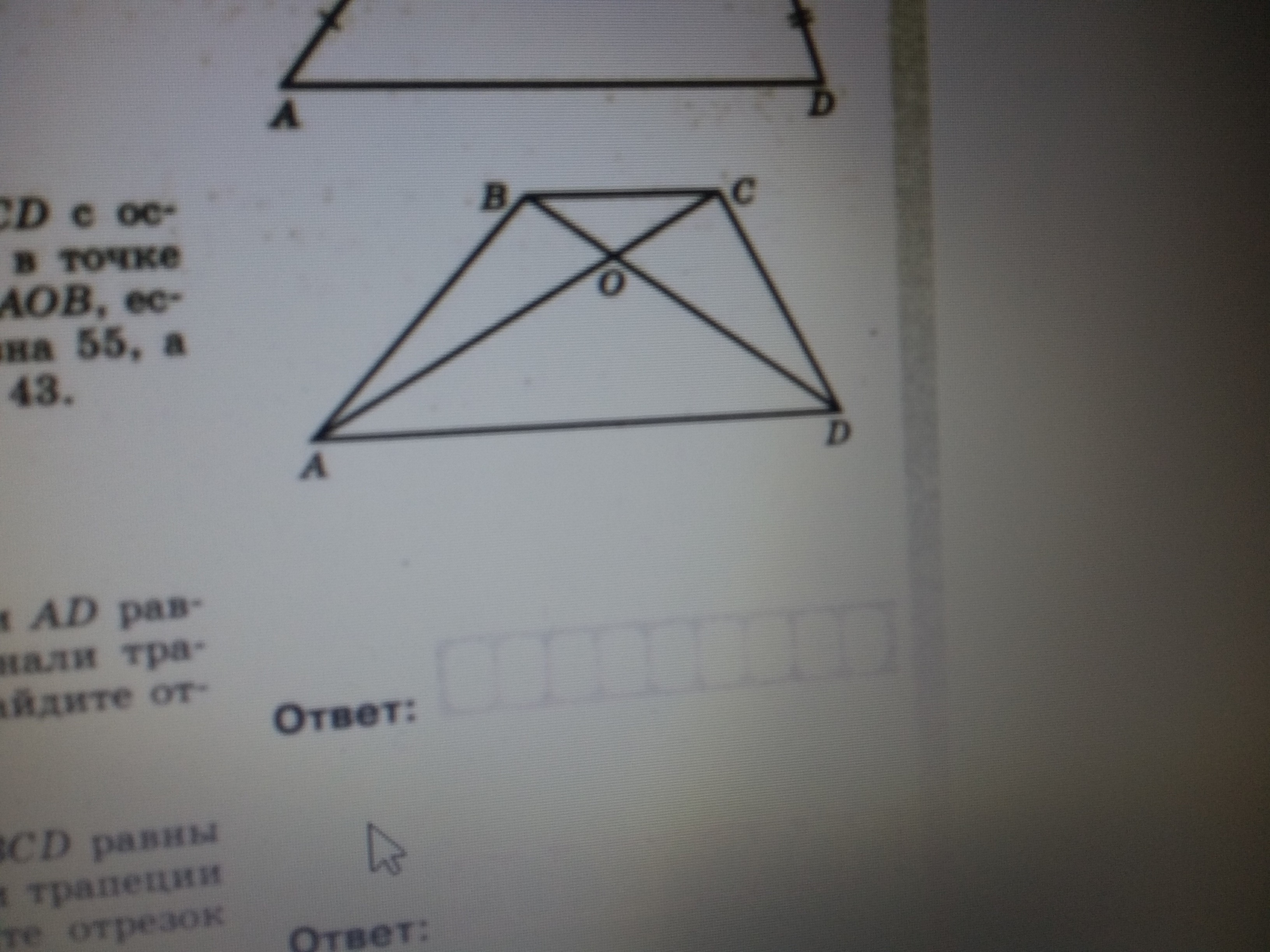














Доказательство равенства треугольников
Для начала, давайте рассмотрим изначальные данные. У нас есть четырехугольник ABCD, в котором AB и CD - параллельные стороны, а AC и BD - диагонали. Также, треугольники АВС и СВАУ имеют общую сторону АС.
Чтобы доказать равенство треугольников, нам необходимо установить равенство их сторон и углов. Рассмотрим:
1. Стороны треугольников: Для этого мы будем использовать информацию о параллельности сторон AB и CD. Из свойств параллельных прямых, мы знаем, что углы между AB и AC, а также между CD и AC, будут равными. Таким образом, сторона AC будет общей для обоих треугольников, а стороны AB и CD будут соответственно равными.
2. Углы треугольников: Для этого мы воспользуемся информацией о диагоналях AC и BD. Из свойств пересекающихся прямых, мы знаем, что углы между AC и AB, а также между AC и CD, будут равными. Таким образом, углы треугольников АВС и СВАУ будут соответственно равными.
Таким образом, мы доказали, что треугольник АВС равен треугольнику СВАУ в четырехугольнике ABCD.
Наши фотографии наглядно демонстрируют каждый шаг доказательства. Это поможет вам лучше понять материал и увидеть связь между данными и выводами.